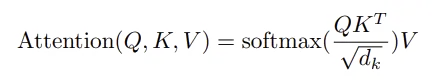Transformers from Scratch in PyTorch
Join the attention revolution! Learn how to build attention-based models, and gain intuition about how they work
Update: I created this GitHub repo containing all of the code from this article, plus basic unit tests: fkodom/transformer-from-scratch
Why Another Transformer Tutorial?
Since they were first introduced in Attention Is All You Need (2017), Transformers have been the state-of-the-art for natural language processing. Recently, we have also seen Transformers applied to computer vision tasks with very promising results (see DETR, ViT). Vision Transformers, for example, now outperform all CNN-based models for image classification! Many people in the deep learning community (myself included) believe that an attention revolution is imminent — that is, that attention-based models will soon replace most of the existing state-of-the-art methods.
All deep learning practitioners should familiarize themselves with Transformers in the near future. Plenty of other Transformer articles exist, both on Medium and across the web. But I learn best by doing, so I set out to build my own PyTorch implementation. In this article, I hope to bring a new perspective and encourage others to join the revolution.
Attention Mechanisms
As the title “Attention Is All You Need” suggests, Transformers are centered around attention mechanisms. Attention is described in the paper’s abstract:
“Attention mechanisms have become an integral part of compelling sequence modeling and transduction models in various tasks, allowing modeling of dependencies without regard to their distance in the input or output sequences.”
In plain English, attention mechanisms relate data points within sequences. And they are very good at doing that.
Transformers use a specific type of attention mechanism, referred to as multi-head attention. This is the most important part of the model! Once you understand multi-head attention, it is pretty easy to understand Transformers as a whole. An illustration from the paper is shown below.
Let’s start with scaled dot-product attention, since we also need it to build the multi-head attention layer. Mathematically, it is expressed as:
What exactly is happening here? Q, K, and V are batches of matrices, each with shape (batch_size, seq_length, num_features). Multiplying the query (Q) and key (K) arrays results in a (batch_size, seq_length, seq_length) array, which tells us roughly how important each element in the sequence is. This is the attention of this layer — it determines which elements we “pay attention” to. The attention array is normalized using softmax, so that all of the weights sum to one. (Because we can’t pay more than 100% attention, right?) Finally, the attention is applied to the value (V) array using matrix multiplication.
Coding the scaled dot-product attention is pretty straightforward — just a few matrix multiplications, plus a softmax function. For added simplicity, we omit the optional Mask operation.
Note that MatMul operations are translated to torch.bmm in PyTorch. That’s because Q, K, and V (query, key, and value arrays) are batches of matrices, each with shape (batch_size, sequence_length, num_features). Batch matrix multiplication is only performed over the last two dimensions.
From the diagram above, we see that multi-head attention is composed of several identical attention heads. Each attention head contains 3 linear layers, followed by scaled dot-product attention. Let’s encapsulate this in an AttentionHead layer:
Now, it’s very easy to build the multi-head attention layer. Just combine num_heads different attention heads and a Linear layer for the output.
Let’s pause again to examine what’s going on in the MultiHeadAttention layer. Each attention head computes its own query, key, and value arrays, and then applies scaled dot-product attention. Conceptually, this means each head can attend to a different part of the input sequence, independent of the others. Increasing the number of attention heads allows us to “pay attention” to more parts of the sequence at once, which makes the model more powerful.
Positional Encoding
We need one more component before building the complete transformer: positional encoding. Notice that MultiHeadAttention has no trainable components that operate over the sequence dimension (axis 1). Everything operates over the feature dimension (axis 2), and so it is independent of sequence length. We have to provide positional information to the model, so that it knows about the relative position of data points in the input sequences.
Vaswani et. al. encode positional information using trigonometric functions, according to the equation:
We can implement this in just a few lines of code:
Note: I’ve gotten several questions about this code. In the equation above, there is a factor of two in the phase exponent. But it is applied at index
2i (+1)in the positional encoding. These factors of two should offset one another, and so I do not include it in my code. I believe this is correct, but it’s possible that I’ve missed something. Please leave me a comment if you see anything that needs fixing. ☺
Now, you may be thinking, “Why use such an unusual encoding? Surely, there are simpler choices!” You’re not wrong, and this was my first thought as well. According to the authors,
We also experimented with using learned positional embeddings instead, and found that the two versions produced nearly identical results. We chose the sinusoidal version because it may allow the model to extrapolate to sequence lengths longer than the ones encountered during training.
Why should sinusoidal encodings extrapolate to longer sequence lengths? Because sine/cosine functions are periodic, and they cover a range of [0, 1]. Most other choices of encoding would not be periodic or restricted to the range [0, 1]. Suppose that, during inference, you provide an input sequence longer than any used during training. Positional encoding for the last elements in the sequence could be different than anything the model has seen before. For those reasons, and despite the fact that learned embeddings appeared to perform equally as well, the authors still chose to use sinusoidal encoding. (I personally prefer learned embeddings, because they’re easier to implement and debug. But we’ll follow the authors for this article.)
The Transformer
Finally, we’re ready to build the Transformer! Let’s take a look at the complete network diagram:
Notice that the transformer uses an encoder-decoder architecture. The encoder (left) processes the input sequence and returns a feature vector (or memory vector). The decoder processes the target sequence, and incorporates information from the encoder memory. The output from the decoder is our model’s prediction!
We can code the encoder/decoder modules independently of one another, and then combine them at the end. But first we need a few more pieces of information, which aren’t included in the figure above. For example, how should we choose to build the feed forward networks?
Each of the layers in our encoder and decoder contains a fully connected feed-forward network, which … consists of two linear transformations with a ReLU activation in between. The dimensionality of input and output is 512, and the inner-layer has dimensionality 2048.
This gives a simple implementation for the Feed Forward modules above:
What kind of normalization should be used? Do we need any regularization, such as dropout layers?
The output of each sub-layer is LayerNorm(x + Sublayer(x)), where Sublayer(x) is the function implemented by the sub-layer itself. … We apply dropout to the output of each sub-layer, before it is added to the sub-layer input and normalized.
We can encapsulate all of this in a Module:
Time to dive in and create the encoder. Using the utility methods we just built, this is pretty easy.
The decoder module is extremely similar. Just a few small differences:
The decoder accepts two arguments (target and memory), rather than one.
There are two multi-head attention modules per layer, instead of one.
The second multi-head attention accepts memory for two of its inputs.
Lastly, we need to wrap everything up into a single Transformer class. This requires minimal work, because it’s nothing new — just throw an encoder and decoder together, and pass data through them in the correct order.
And we’re done! Let’s create a simple test, as a sanity check for our implementation. We can construct random tensors for src and tgt, check that our model executes without errors, and confirm that the output tensor has the correct shape.
Conclusions
I hope this helps to shed some light on Transformers, how they’re built, and how they work. Computer vision folks (like myself) may not have encountered these models before, but I expect to see much more of them in the next couple of years. DETR and ViT have already shown ground-breaking results. It’s only a matter of time before other SOTA models fall to Transformers as well. In particular, I’ll be waiting expectantly on end-to-end attention-based models for object detection, image segmentation, and image generation.